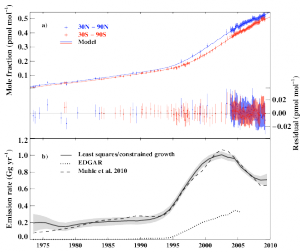
Over the last couple of years, a few of us at MIT and Scripps have been thinking about how we could estimate trace gas emissions over several decades using archived air samples. For example, the Cape Grim Air Archive, from Tasmania, is a really nice collection of air samples that have been taken under carefully controlled conditions over many decades. The archive was set up so that as measurement techniques improved, we could monitor the history of important atmospheric gases that were difficult to measure in the past. We’ve used these observations to determine global emissions of species like the perfluorocarbons (see Jens Muhle’s paper), and some newly-observed HFCs (in Martin Vollmer’s recent paper), all of which are very potent greenhouse gases.
However, one problem that we kept encountering was that, using our usual methods for determining emissions, we would get large ‘jumps’ in our derived emission, which we knew were unlikely to have occurred in the real world. These fluctuations were probably caused by slight biases in the observations, or inaccuracies in the independent emissions inventories that we have to use as a first guess. To get around this problem, we tried to think about how we could derive emissions using information on how we would expect emissions to change from one year to the next. For example, if a gas is emitted by Aluminium smelters, then emissions are not very likely to change by more than a few percent per year, because the number of smelters, or the emissions processes, are unlikely to change very fast.
We found some techniques that addressed similar problems in other fields (notably Oceanography), and modified them so that they could easily be applied to atmospheric trace gas emissions estimation. The result is a method that firstly allows you to estimate the emissions growth rate, based on some prior information, and the uncertainty that you expect this estimate to have. Then a chemical transport model is used to produce an emissions estimate that best matches both the measurements, and our emissions growth constraint. The paper, written with Anita Ganesan and Ron Prinn, can be found here.